Blancos de Reglaje y Tiro - Primera Parte

Dentro de los varios procedimientos que debemos tener en cuenta, uno de los más placenteros es cuando felizmente culminamos con la instalación y el montaje de la mira. Así, obtenemos lo que por definición denominamos la presentación de un conjunto o SAT (Sistema de Armas del Tirador). Ahora, para que nuestro SAT termine de satisfacernos, nos queda una última comprobación, como si fuera este ejercicio la tensión final de la cuerda, para que el instrumento logre deleitar no solo nuestro oído, sino la observación de una buena nota que impacte sobre el blanco.

Pero he aquí un dato fundamental que muchos a veces no teníamos en cuenta, este dato se trata en determinar la corrección real de MOAs o Mrads del mecanismo de corrección de nuestra mira. ¿Porque afirmamos esto? porque no siempre las miras regulan según indican los catálogos de fábrica, sino que mucha de las veces presenta una muy pequeña diferencia de mayor o menor valor en cada clic efectuado.

Esto parecería un dato despreciable, pero no lo es a la hora de regular y disparar a blancos de medianas dimensiones, los cuales nos tomamos el trabajo de medir y ubicar en el terreno para luego realizar precisión en distancias considerables. A veces, la regulación teórica que brindan las tablas de tiro sea se obtengan de los softwares o la que pre confeccionemos, no guardan una relación fiel con los resultados prácticos que se esperan.

Los datos matemáticos si bien son correctos, no concuerdan cuando comenzamos a echar mano a las torretas o discos de corrección de la mira, de modo que el sistema de corrección no funciona en la práctica tal cual lo esperamos. Por lo tanto, debemos analizar los ajustes que ilustra la teoría, para luego reacomodar nuestros cálculos, estableciendo en verdad que corrección real de campo posee nuestro sistema óptico, cuando comenzamos a mover las torretas con el fin de llegar a las medidas angulares (MOAs o MRADs) correspondientes. Este es el principal objetivo de la utilización del blanco de reglaje, a fin de asegurar la corrección real de la mira, y de esta manera diseñar la construcción que involucren la confianza del correcto el ajuste y corrección de las tablas balísticas y de tiro.

El blanco de reglaje debe presentar una red de cuadrados, extremadamente precisos en las medidas y sistemas angulares elegidos. Es común ver tiradores que disparan a blancos de 1" (2,54 cm) a 150 metros, esto no tiene sentido, debido a que como mencionamos la finalidad del blanco de reglaje es comprobar la mecánica de la mira y la precisión de nuestro SAT sobre el blanco.

En todo caso, para una distancia de 150 m, las medidas de los cuadrados deberían tener 4,36 cm. Pero esto ocurre en polígono de Argentina, en ningún otro polígono ponen a cero el sistema de armas en 150 m, sino que lo hacen en distancias redondas 100m,200m,300m,500m, dependiendo del calibre.

No ocurre eso con los blancos que presentamos, estos poseen medidas de 1 MOA a 100 m (2,91 cm) cada cuadrado y de 2 cm para miras que regulan en MRADs.

Así podemos observar

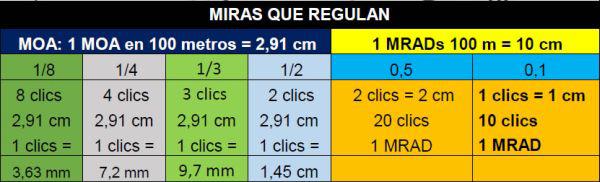
Como Determinar el Error de Arrastre y Parámetros para el Uso del Blanco de Reglaje

Este blanco permite trabajar tres (3) aspectos en la búsqueda de puesta a punto del SAT Sistema de Armas del Tirador:

1) Identificar y corregir los Errores de Impactos tanto de Altura como de Deriva sobre nuestro blanco de reglaje, el cual posee una grilla o red de cuadrados con las medidas exactas para la lectura de valores angulares (MOAs) los que en términos matemáticos deberían coincidir con el sistema de corrección de la mira a la hora de moverlas o girarlas con el fin de obtener centros y precisión en la distancia de tiro.

2) Comprobar si la mecánica de corrección de las torretas o discos de la mira guarda relación con las medidas correctas referidas en el blanco.

3) Determinar el Error de Arrastre del mecanismo de corrección: muchas veces la mira posee un denominado "Error de Arrastre" y la única manera de corroborarlo, es someter a la mira una vez que se realizó la puesta en "CERO" mediante el empleo del Método del Cuadrado, El tirador realizara justes de manera intencional sobre nuestro blanco pensado y optimizado, de manera que los movimientos de 10 MOAs UP (Arriba) -10 MOAs "R" (Derecha) 10 MOAs Down (Abajo) y 10 MOAs "L" (Izquierda) determinen si al disparan sobre el blanco, estos movimientos y los valores matemáticos para llegar a la corrección optima difieren de las medidas angulares que deberían adoptar en la distancia de regulación y tiro.

Comprobación de Error de Arrastre

Una vez regulado el SAT, el tirador procederá a verificar la corrección de la mira empleando el método del Cuadrado que explicaremos a continuación.

Sabemos que, aplicando el método del cuadrado sobre un blanco a una distancia determinada, ejemplo 100 metros y moviendo 10 MOAs a cada vértice, debería existir una equidistancia de 29,1 cm (teórico).

El problema puede presentarse cuando el tirador decide realizar la comprobación de tiro en el campo, a veces se encuentra con una realidad distinta a la que indica la lógica y la teoría.

Suponiendo que en vez de correr 10 MOAs = 29,1 cm en 100 metros, el tirador comprueba al medir los impactos en el blanco una constante de equidistancia de 35 cm.

Al efectuar movimientos de 10 MOAs en las torretas aplicando el método del cuadrado difiere, en vez de 29,1 centímetros como indica el cuadro teórico.

Si tomamos este ejemplo y su resultado, comprobaríamos rápidamente que 1 MOA en nuestra mira corrige 3,5 centímetros en vez de 2,91 que es lo que matemáticamente y en teoría debería.

Corrección Ideal

10 MOAs ----------- 29,1 cm ------------- 100 metros a cada vértice del cuadrado.

Corrección Real de Comprobación en Campo de Tiro

B) 10 MOAs ----------- 35 cm ------------- 100 metros a cada vértice del cuadrado.

Diferencia

Dif= 35 cm reales - 29,1 ideal = 5.9 cm en 100 metros por cada 10 MOAs
Dif = 3,5 cm - 2,91 = 0.59 cm poco más de medio centímetros en 100 metros por cada 1 MOA aplicado

R: 5,9 centímetros en 100 metros por cada 10 MOAs o 5,9 mm por cada MOA de error mismo registro en intención de corrección.

Ahora para ejemplificar como influiría este "Error de Arrastre" tomemos la corrección real de comprobación en el campo de tiro.

Si tomamos en cuenta estas medidas, deberíamos establecer para nuestros cálculos, el valor real que posee 1 MOA de corrección en nuestra mira, al igual que el valor de cada clik´s. (todavía estamos analizando)

Ejemplo de Regulación y Diferencia Mecánica por Error de Arrastre

Ahora, partamos de un ejemplo con un calibre .308, peso de punta 168 grains, CB G1: 0,447, velocidad inicial de 2531 fps ? Fusil SAKO mod TRG-21 paso de Estria:1:11" ? en condiciones Atmosféricas ISA.

• Temperatura 15 °C
• Altitud: 0 NM.
• Presión: 760 Hg mm

Regulación sugerida en 1000 metros.

Regulación Ideal Sin Error de Arrastre

Esta sería la corrección con una mira que corrige dentro de los parámetros teóricos normales.

• Drop = 39,752 MOAs x valor Ideal 1 MOA en la distancia de tiro 1. 000 m 29,1 cm o 0,291m)
• Drop = 39,752 MOAs x 0,291m = 11,567 m de caída

Regulación Real con la Mira considerando el Error de Arrastre

Si el tirador regulase 39,752 MOAs que es lo sugerido para contrarrestar una caída de 11,567 m del proyectil en 1.000 metros, no teniendo en cuenta el error de arrastre de su mira, la diferencia en el punto de impacto pretendido seria notable y deberíamos determinar la diferencia.

• 1 MOA real en la mira comprobado en el blanco de reglaje
• 1 MOA = 3,5 cm en 100 metros
• 1 MOA = 35 cm en 1000 metros
• Drop = 39,752 MOAs x Valor Real (como se comprobó que corrige la mira)1 MOA según distancia de tiro y los errores sobre el blanco de reglaje.
• Drop = 39,752 MOAs x 0,35 = 13,913 m de caída proyectil en 1.000 metros de distancia

Diferencia Entre Regulación Ideal y Real de Campo

• Diferencia de Drop = Ideal - Real = (13,913 - 11,567 = 2,346 m)
• Corrección de la mira 1/4 MOA: 39,752 x 4 = 159 clics
• Diferencia de valor de cada clic = 0.59 x 39,752 MOAs = 23,45 cm de error arrastre en la totalidad de corrección.
• Diferencia de MOAs = 23,45 cm / 29,1 cm (valor de 1 MOA 1.000 m) = 0,805 MOAs de diferencia

Comprobación

• Tg 0,805 (MOAs) /60 x 1000 metros = 23,45 cm

De modo que el disparo poseerá un error de 23,45 centímetros en 1.000 metros de distancia, sin tener en cuenta la suma de otros factores como el Drift (desvió por rotación angular), viento, etc., provocará la imprecisión sobre el blanco seleccionado.